端到端的机器学习项目之探索数据（Machine Learning 研习之七）

本篇其实是承接上一篇内容，之所以没在上一篇将它写完，那是有原因的，毕竟，本着学习的态度，篇幅不应过长，方能使你有学习的欲望！

探索数据

首先，确保你已经把测试放在一边，你只是在探索训练集。此外，如果训练集非常大，您可能希望对探索进行采样设置，使操作在勘探阶段变得容易和快速。在这种情况下，培训集非常小，所以您可以直接处理完整集。由于你要试验完整训练集的各种变换，你应该制作一份原始的所以你可以在之后恢复它:

housing = strat_train_set.copy()

可视化地理数据

因为数据集包括地理信息(纬度和经度)，所以创建一个所有地区的散点图来可视化数据是一个好主意(见下图):

housing.plot(kind="scatter", x="longitude", y="latitude", grid=True)
plt.show()

这看起来很像加州，但除此之外，很难看到任何特别的模式。将alpha选项设置为0.2可以更容易地显示数据点密度高的位置(见下图):

housing.plot(kind="scatter", x="longitude", y="latitude", grid=True, alpha=0.2)
plt.show()

现在的情况要好得多:你可以清楚地看到高密度地区，即海湾地区、洛杉矶和圣地亚哥周围，再加上中央山谷(特别是萨克拉门托和弗雷斯诺)的一长排高密度地区。

我们的大脑非常善于发现图片中的模式，但你可能需要玩弄可视化参数，使模式脱颖而出。

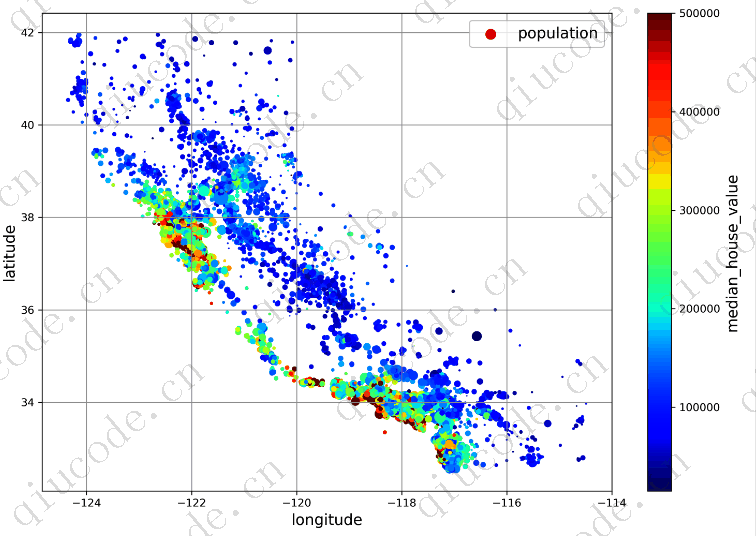
接下来，你再看看房价(见下图)。每个圆圈的半径代表该地区的人口(选项s)，颜色代表价格(选项c)。这里使用了一个名为jet的预定义颜色映射(选项cmap)，其范围从蓝色(低值)到红色(高价):s

housing.plot(kind="scatter", x="longitude", y="latitude", grid=True,
s=housing["population"] / 100, label="population",
c="median_house_value", cmap="jet", colorbar=True,
legend=True, sharex=False, figsize=(10, 7))
plt.show()

这张图告诉你，房价与地理位置(例如，靠近大海)和人口密度密切相关，你可能已经知道了。聚类算法对于检测主集群和添加测量与集群中心的邻近性的新特性应该是有用的。海洋邻近属性也可能是有用的，尽管在北加州沿海地区的房价不是太高，所以这不是一个简单的规则。

寻找相关性

由于数据集不是太大，你可以很容易地使用corr()方法计算每对属性之间的标准相关系数(也称为皮尔逊相关系数):

corr_matrix = housing.corr()

现在您可以查看每个属性与房屋中值的相关性:

相关系数从-1到1。当它接近1时，意味着有很强的正相关关系，例如，当收入中位数上升时，房屋价值中位数往往会上升。当系数接近-1时，意味着有很强的负相关性;你可以看到纬度和房屋价值中间值之间有一个很小的负相关性(即往北走，房价有轻微的下降趋势)。最后，系数接近0意味着不存在线性相关关系。

检查属性之间相关性的另一种方法是使用Pandas scatter_matrix ()函数，该函数将每个数值属性与其他每个数值属性进行绘图。由于现在有11个数字属性，您将得到112=121幅不适合页面的地块，所以您决定将重点放在一些看起来与住房中值最相关的有前途的属性上(见下图):

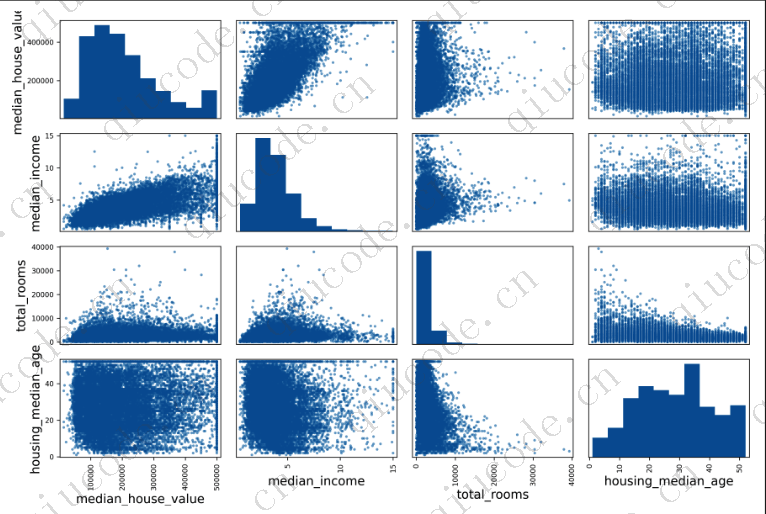
如果Pandas将每个变量相对于自身绘制，那么主对角线将充满直线，这将不是很有用。因此，Pandas显示每个属性的直方图(其他选项可用;请参阅Pandas文档以获取更多详细信息)。

查看相关散点图，似乎最有希望预测房屋价值中位数的属性是收入中位数，所以你放大他们的散点图(见下图):

housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1, grid=True)
plt.show()

这个情节揭示了一些事情。首先，相关性确实很强;你可以清楚地看到上升的趋势，而且点也不太分散。第二，你之前注意到的价格上限在500，000美元的水平线上明显可见。但这个情节也揭示了其他不那么明显的直线:一条水平线在45万美元左右，另一条大约35万美元左右，也许还有一条大约28万美元，还有几条低于这一点。您可能希望尝试删除相应的区域，以防止您的算法学习重现这些数据怪癖。

警告：

相关系数只测量线性相关性(“当x上升时，y通常上升/下降”)。它可能会完全忽略非线性关系(例如，“当x接近0时，y通常会上升”)。图2-16显示了各种数据集及其相关系数。请注意，尽管它们的轴线显然不是独立的，但底部行的所有图都具有等于0的相关系数:这些都是非线性关系的例子。另外，第二行显示了相关系数等于1或-1的示例;注意，这与斜率无关。例如，以英寸为单位的身高与以英尺或纳米为单位的身高的相关系数为1。