当您看到本文标题时，不禁感叹，总算是到了
训练模型这一节了。是啊，在之前的文章中，我们对数据进行了探索，以及对一个训练集和一个测试集进行了采样，也编写了一个
预处理管道来自动清理，准备您的数据用于机器学习算法，然而现在，我们可以选择并训练模型了。
训练集的训练与评估
我们从一个最基本的线性回归模型开始：
from sklearn.linear_model import LinearRegression
lin_reg = make_pipeline(preprocessing, LinearRegression())
lin_reg.fit(housing, housing_labels)
很好，至此，我们现在算是有了一个有效的线性回归模型，可以在训练集上试用它，查看前五个预测，并将它们与标签进行比较:：
第一个预测偏差很大(超过200,000美元!)，而其他预测则更好，两个预测偏差约25%，还有两个预测
偏差不到10%。请记住，您选择使用RMSE作为性能测度，因此您希望使用Scikit-Learn的mean_squared_error()函数在整个训练集上测量该回归模型的RMSE，并将平方参数设置为False。
这总比没有好，但显然不是一个很好的分数，大多数地区的房屋价值中位数在120,000美元和26.5万美元之间，所以一个典型的68628美元的预测误差真的不是很令人满意。这是一个模型拟合训练数据不足的示例。当这种情况发生时，可能意味着这些特征没有提供足够的信息来做出好的预测，或者模型不够强大。
正如我们在上一章中看到的，修复欠拟合的主要方法是选择一个更强大的模型，为训练算法提供更好的特征，或者减少对模型的约束。这个模型没有正规化，这就排除了最后一个选项。您可以尝试添加更多功能，但首先您要尝试更复杂的模型，看看它是如何工作的。
您决定尝试DecisionTreeRegressor，因为这是一个相当强大的模型，能够在数据中找到复杂的非线性关系(后续篇章将更详细地介绍决策树)：
from sklearn.tree import DecisionTreeRegressor
tree_reg = make_pipeline(preprocessing, DecisionTreeRegressor(random_state=42))
tree_reg.fit(housing, housing_labels)
现在模型已训练完毕，您可以在训练集中对其进行评估：
等等，难道这个模型真的很完美吗？当然咯，更有可能的是模型严重地过度拟合了数据。您怎么能确定正如你前面看到的，在您准备好启动一个您有信心的模型之前，您不想碰测试集，所以您需要使用一部分训练集进行训练，另一部分用于模型验证。
使用交叉验证进行更好的评估
评估决策树模型的一种方法是使用train_test_split()函数将训练集拆分为较小的训练集和验证集，然后针对较小的训练集训练您的模型，并针对验证集对其进行评估。这是一点努力，但没有太难，它会工作得相当不错。
一个很好的替代方法是使用Scikit-Learn的k_-fold交叉验证特性。下面的代码随机地将训练集分成10个不重叠的子集，称为fold，然后训练和评估决策树模型10次，每次选择不同的fold进行评估，并使用其他9个fold进行训练。结果是一个包含10个评价分数的数组：
from sklearn.model_selection import cross_val_score
tree_rmses = -cross_val_score(tree_reg, housing, housing_labels,
scoring="neg_root_mean_squared_error", cv=10)
警告：
Scikit-Learn的交叉验证功能期望的是效用函数(越大越好)而不是成本函数(越低越好)，所以评分函数实际上是RMSE的反面。它是一个负值，所以您需要切换输出的符号来获得RMSE分 数。
让我们来看看结果吧：
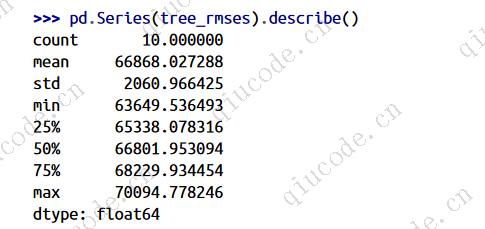
现在决策树看起来不像以前那么好了。事实上，它的表现几乎和线性回归模型一样差！请注意，交叉验证不仅允许您获得模型性能的估计值，还允许您测量该估计值的精确度(即其标准差)。决策树的均方根误差约为66，868，标准差约为2,061。如果只使用一个验证集，则不会有此信息。但是交叉验证是以多次训练模型为代价的，所以它并不总是可行的。
如果您为线性回归模型计算相同的度量，您将发现平均RMSE为69，858，标准差为4,182。因此，决策树模型的性能似乎比线性模型稍微好一点，但由于严重的过拟合，差异很小。我们知道存在过拟合 问题，因为训练误差很低(实际上为零)，而验证误差很高。
现在让我们尝试最后一个模型:随机森林调节器，随机森林的工作原理是在特征的随机子集上训练许多决策树，然后平均出它们的预测值。这样的模型组成的许多其他模型被称为合奏:他们能够提高性能基础模型(在本例中为决策树)。代码与前面的代码大同小异：
from sklearn.ensemble import RandomForestRegressor
forest_reg = make_pipeline(preprocessing,
RandomForestRegressor(random_state=42))
forest_rmses = -cross_val_score(forest_reg, housing, housing_labels,
scoring="neg_root_mean_squared_error", cv=10)
随机森林真的看起来非常有前途的任务！但是，如果您训练一个RandomForest并测量训练集上的RMSE，您将发现大约17，474:这要低得多，这意味着仍然存在大量的过度拟合。可能的解决方案是
简化模型，约束它(即，规则化它)，或得到更多的训练数据。但是，在深入研究随机森林之前，您应该尝试来自各种类别机器学习算法的许多其他模型(例如，具有不同内核的多个支持向量机，可能还有一个神经网络)，而无需花费太多时间调整超参数。目标是列出几个(两到五个)有前途的模型。